MANUAL |
TOP PAGE |
LINK |
| メニュー | |||
| 数理モデル | |||
| 数理モデルによる分析と予想とは | |||
| 確率とゲーム理論 | |||
| KHRIのグラフの見方 | |||
| 人工知能 | |||
| 株価分析 | |||
| 株価予測 | |||
| 株価予想 | |||
| 株式投資 | |||
| 投資情報 | |||
| 銘柄選び | |||
2020年4月12日
最近よく耳にする「数理モデルによる予測」は、数値化された過去のデータをもとに数式によるモデルを構築し、それを用いて未来を予想していく技術である。コンピュータ性能や分析技術の向上により目覚ましく発展しつづけている。このサイトでは、経済活動に基づく市場の動きを数理モデル化し将来の動きを予測計算した結果をわかりやすいグラフでご覧いただく事ができます。
数理モデルとはおおまかに説明すると数学で習ったような数式のことです。数式とは、簡単な例でいうと、1次関数や二次関数、サイン関数やコサイン関数などです。過去のデータの動きを数理モデル(数式)化することができれば、その数理モデルを用いて未来を予測する事ができます。
簡単な問題で未来予測について考えてみましょう。次の問題をみてください。
| 問題: | ||
| A君は自転車で家を出発し、30分後に家から直線距離で6000mの場所に到達しました。A君が家を出発してから45分後に自転車で走る距離を求めなさい。 |
これはまさにA君が走る距離の未来予測です。A君は30分で6000m走ったので、単純に考えると1分あたり200m(=6000/30)となります。45分間で走る距離を計算するので、答えは 200×45=9000m と考えられます。
これが数学の問題であったならば、問題としてかなり不完全で解く事ができません。まず、A君は一定速度で走ったのか?直線距離とA君の走る距離の関係は?つまりA君は家から真っ直ぐに走ったのか?などが疑問として浮かびます。
A君がくねくねと曲がった山道を走っていたら、家から直線距離で6000mの場所は実際に走った距離では何倍にもなるかもしれません。A君が一定速度ではなくて早く走ったりゆっくり走ったりしていた場合には単純に1分間に200mの速度ではなくなるし、その後の15分も同じ速度で走るとは限りません。したがって、これが数学のテストの問題だったならば、これだけの情報で完全な答えを出す事は不可能です。
先ほどのA君の問題を数学のテストの問題として解くことが困難なのは理解いただいたと思います。この問題を解くには、前提を置いて計算をする必要があります。「A君は休まずに一定の速度で直線の道路を走行した」という前提を置けば解くことができます。A君の走った距離 y は、時間をx分として、y=Ax+B という形で数理モデルを構築できます。数理モデルのパラメタ「A」と「B」は、問題中の、 (家を出発した) 0分 で距離 0m 、30分後に距離6000mという過去のデータから、A=200、b=0 と推定できます。
未来予測した結果を何に使うかによって、考えなくてはいけない前提の精度と、それにより得られる結果の精度が変わります。あなたが数百メートル離れた場所からA君を狙撃するスナイパーなら、数センチ単位の正確なA君の位置が必要です。または、あなたが逃走したA君を追跡する警察官なら、おおよそのA君の逃走距離が数km以内に絞れるだけでも犯人追跡のための有力な情報になるでしょう。その様な極端な例でなくても、日常の生活の中では確率的な大雑把な情報でも何かを判断するのに十分に役立つ情報になりえるでしょう。
先ほどのA君の問題の数理モデル構築は、大きく分けると2つのステップに分ける事ができる。1つ目は、妥当性の高い前提を置き(仮説構築)、数理モデルを構築するステップ。2つ目は、過去のデータを用いて数理モデルのパラメタを合わせるステップ(パラメタ学習)です。
この中で、2つ目のパラメタ学習は、数理モデルと過去のデータがあれば数学的手法に則って機械的作業で実施できますが、最初のステップである仮説設定と数理モデル構築が極めて重要となります。前提や数理モデルは粗すぎても詳細すぎても未来を予測する性能が低下してしまいます(汎化性能の低下)。荒すぎる数理モデルでは未来の予測値のズレが大きくなるのは簡単に想像できます。逆に詳細すぎる数理モデルでも過去のデータとはよく一致するが過去のデータに必要以上に一致させすぎて将来の予測がうまくできない場合があります。いかに適切な仮説を用いて数理モデルを構築できるかが、未来予測のカギとなります。
先ほどのA君の問題でもあったように、前提を考えることが重要になります。現実の世界では、完全に一定速度で自転車を走らせる事はないし、完全に真っ直ぐな直線道路もほぼ存在しません。なので、前提を考える事は、近似を考えることと等しくなります。完全な未来予測を行う事はできませんが、30分間で6000m走った人が次の15分間で3000m走るであろうことは近似としては妥当だと言えるでしょう。もちろん、与えられる情報が変われば予測も変わります。たとえば、平均的に直線距離と実際の走行距離が約2倍異なるという情報が得られたとすると、A君は30分間で 6000m×2倍の距離を走ったことになるので、先ほどの答えも2倍になります。
また、未来予測の結果が確率的な近似であるため1つ1つの個別の事象では当たったり外れたりしますが、確率の性質上、数が多くなれば結果との平均値での一致度は高くなります。つまり、A君のみではなく、例えば家を自転車で出てからの移動距離の走行データを1万人分用意して数理モデルを構築し、同様な属性(地域や年齢)の別の2000人について未来予想した結果の平均値を評価すれば、1人に対して実施した未来予想よりも結果の精度は高くなる傾向があります。
パラメタ学習は数理モデルと過去のデータがあれば数学的手法に則って機械的作業で実施できると述べましたが、学習のためのパラメタもあります。学習のためのパラメタは、例えば何年分のデータを使うかや、データの重み付けなどです。一般的にパラメタ学習を行うには、学習のためのパラメタを変更して既に結果がわかっているデータで検証して、検証結果が最も良くなるように最終的な学習のためのパラメタを決定します。
また、未来予測においては、数理モデルのパラメタ学習に用いる過去のデータが時間と共に増えるので、数理モデルのパラメタや未来予測の結果も、刻一刻と変化します。
未来予想の仕組みは、過去のデータから変化のベースとなっている要素を反映した数理モデルを構築し、その要素による影響を未来へ向かって数式で解くことで予想を行います。予測結果は過去のデータから予測した確率的な傾向を示しています。
市場予測での背景となる考え方は、世の中の経済活動などはランダムな動きをしているのではなく、人の活動や物流などのモノの動き、設備投資や設備の劣化など、複数の周期的な要因が組み合わさった結果として経済データが動きます。経済活動の結果として現れてくる過去のデータを用いて、背景となる経済活動の要素を反映した数理モデルを構築することで未来を予測します。従って、この手法の限界は、数理モデル構築に使用した過去のデータに含まれていない未知の活動や要素(メカニズム)が発生したときに影響を予測できない点です。KHRIの株価予測は、おおよそ過去30年のデータから数理モデル構築とパラメタの学習をおこなっています。従ってそれ以上の周期で発生する事象や偶発的な事象による影響は予測に織り込まれません。例えば極端な例では、10万年に1度の火山活動で経済の大損失が出るとか、1億年に1度の隕石衝突で甚大な被害が出て経済が落ち込む事などが発生したら、今回の方法では予測できません。
突然ですが、大型投資銀行の経営破綻に端を発した世界規模の金融危機を、過去データから構築した数理モデルにより予測する事は可能でしょうか?
前の章で説明した様に、過去データに反映されていない未知のメカニズムによる影響は予想できません。では、その金融危機は未知のメカニズムによる影響だったのでしょうか、という事が重要になります。
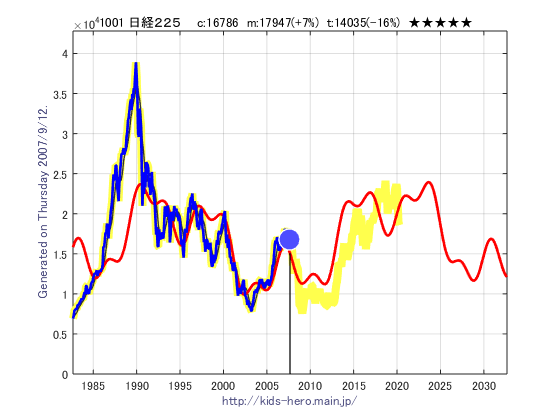
事実として、2008年9月に発生した米国の投資銀行リーマン・ブラザーズの経営破綻に端を発した金融危機=リーマンショックによる市場の下落を、KHRIの数理モデルは予測していました。下のグラフはリーマンショックの1年前である 2007年9月時点の日経平均の予想です。青線はその時点での過去データ、赤線は数理モデルによるその時点での予測値、太い黄船は後から検証の為に追加した実際のデータです。この図の結果では、リーマンショックの1年前の株価が16786円の時点で、その後に約10000円への下落(赤線)を予想していまいした。実際にはその1年後の2008年10月に8577円まで下落しました(黄線)。値のズレはあったものの、下落する事は予想できていました。
|
|
では、何故、KHRIの数理モデルはリーマンショックを予測できたのでしょうか。それはリーマンショックが未知のメカニズムや予測不能な突発的な事故として発生したのではなく、従来の経済メカニズムの中で発生していたと考えるのが自然です。つまり、リーマン・ブラザーズの経営破綻が金融危機の原因となったのではなく、市場はそのとき既に下落のポテンシャルを持っていて、リーマンショックはその下落を開始するトリガーでしかなかったということです。リーマンショックの背景に従来の経済メカニズムがあったからこそ、従来の経済メカニズムによる過去データから構築されたKHRIの数理モデルで予想が可能だったのです。
下の図は、リーマンショックの更に5年前である 2003年9月時点の日経平均の予想です。この時点ではまだ10219円だったにも関わらず既にその後の17000円付近までの上昇と、その後のリーマンショック付近の1万円近辺への下落を予想できています。更にリーマン・ショック後の2015年付近の2倍近くの上昇も、10年以上先の予想にも関わらずほぼ正確に予測できています。こうして見るとリーマン・ブラザーズの経営破綻で金融危機が起こったのではなく、その逆でもともと経済の下落があってそれが原因でリーマン・ブラザーズが経営破綻したのかもしれません。
|
|
上記の2003年9月時点の予想グラフは、当然の事ながら2003年9月時点までのデータのみ用いて予測を行っているにも関わらず、2020年4月の現時点で見てもその後の日経平均の大まかな傾向を予測出来ていることに驚きます。この事は、経済活動が経営破綻や先のわからぬ景気動向などの突発的な事象に左右されているように見えても、実はそれらの出来事は従来起こるべき現象がはじまる為のきっかけでしかなく、経済の大きな動き(メカニズム)が全体の動きを支配していると言えるでしょう。
下の図は、現時点(2020年3月)の図です。2027年頃に一度ピークがあり、そこから2030年あたりにかけて60%の下落をしていく予想が出ています。この先どんな経済の事件がきっかけで市場が転換し動き始めるかはわかりませんが、将来大きな天災や大企業の破綻がきっかけで市場が動いたように見えたとしてもそれらは単なるトリガーでしかなく、市場の大まかな動きはすでに経済の大きなサイクルの中で方向づけられているのではないかと考えられます。
|
|
*資料提供:Kids-Hero Research Institute.